实时称重卡尔曼滤波：精准测量的关键技术

引言

在现代工业和科研领域，实时称重技术在质量监控、自动化生产线等方面扮演着至关重要的角色。然而，由于环境因素和测量设备的限制，传统的称重系统往往难以实现高精度和高稳定性的测量。卡尔曼滤波作为一种先进的信号处理技术，被广泛应用于实时称重系统中，以提升测量精度和稳定性。本文将深入探讨实时称重卡尔曼滤波的原理、实现方法及其在实际应用中的优势。

卡尔曼滤波简介

卡尔曼滤波是一种有效的递归滤波算法，由美国科学家鲁道夫·卡尔曼于1960年提出。它适用于线性动态系统和线性观测模型，能够通过最小化误差方差来估计系统状态。卡尔曼滤波的核心思想是利用先前的估计值和当前观测值来更新状态估计，从而实现动态系统的实时跟踪。

实时称重系统中的卡尔曼滤波

1. 系统模型

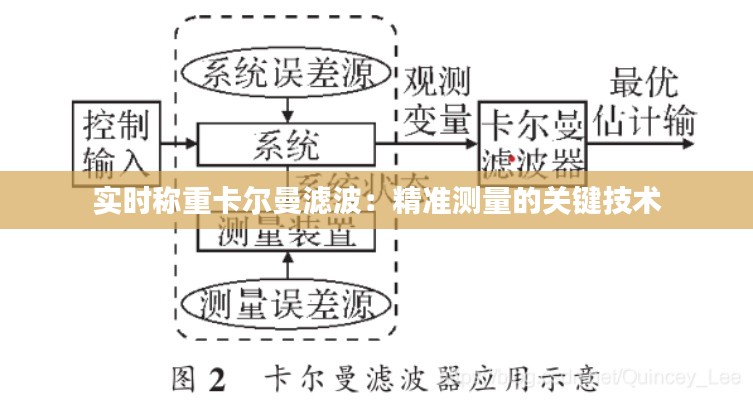
实时称重系统通常由传感器、信号采集和处理单元以及控制单元组成。传感器负责测量物体的重量，信号采集和处理单元将传感器输出的模拟信号转换为数字信号，并对其进行初步处理，最后由控制单元进行状态估计和决策。

在卡尔曼滤波中，系统模型可以表示为以下形式：

[ x_{k+1} = A \cdot x_k + B \cdot u_k + w_k ]

[ y_k = C \cdot x_k + v_k ]

其中，( x_k ) 表示第 k 时刻的系统状态，( u_k ) 表示系统输入，( w_k ) 和 ( v_k ) 分别表示系统噪声和观测噪声，( A ) 和 ( C ) 为系统矩阵。

2. 卡尔曼滤波算法

卡尔曼滤波算法主要包括预测和更新两个步骤。

• 预测：根据先前的估计值和系统模型，预测当前时刻的系统状态。

[ \hat{x}k|k-1 = A \cdot \hat{x}{k-1|k-1} ]

[ Pk|k-1 = A \cdot P{k-1|k-1} \cdot A^T + Q ]

其中，( \hat{x}_k|k-1 ) 表示第 k 时刻的系统状态预测值，( P_k|k-1 ) 表示预测协方差矩阵，( Q ) 为过程噪声协方差矩阵。

• 更新：根据当前观测值和预测值，更新系统状态估计。

[ K_k = P_k|k-1 \cdot C^T \cdot (C \cdot P_k|k-1 \cdot C^T + R)^{-1} ]

[ \hat{x}_k|k = \hat{x}_k|k-1 + K_k \cdot (y_k - C \cdot \hat{x}_k|k-1) ]

[ P_k|k = (I - K_k \cdot C) \cdot P_k|k-1 ]

其中，( K_k ) 为卡尔曼增益，( y_k ) 表示第 k 时刻的观测值，( R ) 为观测噪声协方差矩阵，( I ) 为单位矩阵。

实际应用中的优势

实时称重卡尔曼滤波在实际应用中具有以下优势：

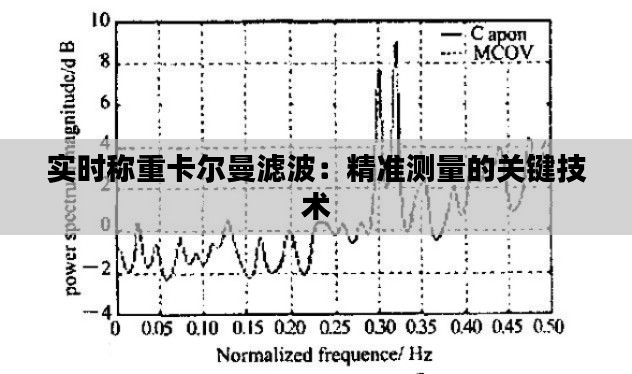
• 高精度：卡尔曼滤波能够有效抑制噪声和干扰，提高测量精度。
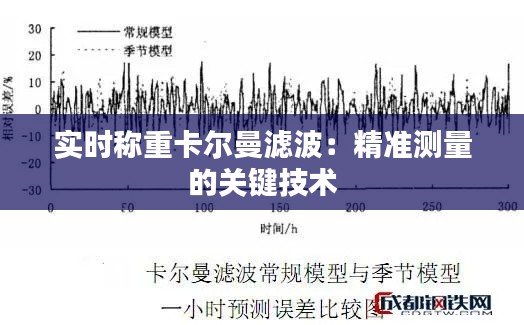
• 实时性：卡尔曼滤波算法具有递归性质，能够实时更新系统状态估计。
• 鲁棒性：卡尔曼滤波对系统模型和噪声统计特性的变化具有较强的适应性。

总结

实时称重卡尔曼滤波作为一种先进的信号处理技术，在提高称重系统精度和稳定性方面具有显著优势。随着技术的不断发展和应用领域的拓展，卡尔曼滤波将在更多领域发挥重要作用。

参考文献

[1] 卡尔曼，R. E. (1960). A new approach to linear filtering and prediction problems. Journal of Basic Engineering, 82(1), 35-45.

[2] 胡寿松. (2001). 随机信号处理. 北京：清华大学出版社.

[3] 李航. (2008). 统计学习方法. 北京：清华大学出版社.